EJERCICIOS PARA PRACTICAR

Ahora que ya conoces el tema y en que consiste, se presentan a continuacion algunos ejercicios que te serviran para poder practicar el conocimineto aquirido.

DEMOSTRACIÓN DEL TEOREMA

DEMOSTRACIÓN DEL TEOREMA

para que el tema se pueda entender de una mejor manera, a continuación se presentan algunos vídeos del como el teorema de tales es aplicado:

Si bien el teorma puede ser aplicado en diversas areas de nuestra vida cotidiano. Ya hemos dado un ejemplo anteriormente. Un ejemplo puede ser, cuando nosotros queremos saber la altura de una cosntruccion, y para saberlo nos basamos en un objeto que servira de parametro, asi como las sombras que ambos generen para poderlo calcular.

TEOREMA DE TALES DE MILETO

EL teorema de Tales se considera el teorema fundamental de la semejanza  de triángulos y establece lo siguiente:

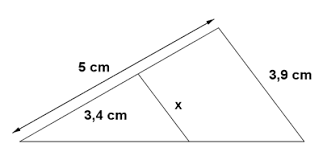
Toda recta paralela a un lado de un triángulo, forma con los otros dos lados o con sus prolongaciones otro triángulo que es semejante al triángulo dado.

Cuando en geometría hablemos del Teorema de Tales (o Thales) , debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

Primer teorema Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.Entonces, veamos el primer Teorema de Tales en un triángulo

THALES Y LA PIRÁMIDE DE KEOPS

Alrededor del año 600 a.C., Thales visitó Egipto, donde el faraón; que había oído hablar de la inteligencia de Thales; le pidió que averiguara la altura de la Gran Pirámide de Keops. 

Para ello, nuestro gran sabio, clavó su bastón en el suelo de forma vertical y esperó… En el instante justo en el que la sombra de su bastón fue igual a la altura del bastón, entonces la sombra de la pirámide también sería igual a la altura de ésta. Suponemos que para poder llevar a cabo este experimento, recibiría ayuda de alguien. Cuando en geometría hablemos del Teorema de Tales (o Thales) , debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

TEOREMA

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.

Introduccion

INTRODUCCION: MATEMATICAS

Matemática. (del Latín mathematĭca, y éste del Idioma griego μαθηματικά, derivado de μάθημα, Conocimiento) es una ciencia que, a partir de notaciones básicas exactas y a través del razonamiento lógico, estudia las propiedades y relaciones cuantitativas entre los entes abstractos (números, figuras geométricas, símbolos). Mediante las matemáticas conocemos las cantidades, las estructuras, el espacio y los cambios. Los matemáticos buscan patrones,[1] formulan nuevas conjeturas e intentan alcanzar la verdad matemática mediante rigurosas deducciones. Éstas les permiten establecer los áxiomas y las definiciones apropiados para dicho fin.

COLEGIO DE BACHILLERES DEL ESTADO DE PUEBLA

PLANTEL 27----------ZARAGOZA, PUEBLA

MATEMÁTICAS II

ALUMNO: BRAULIO DENAIN LUNA RONQUILLO

PROFESOR: ARQUIMIDES OSORIO ROMERO

CICLO ESCOLAR: 2018